SophSem210: Notes for class 4

Notes for Class 4

Force of a Spring

• Springs obey Hooke's law.
• Force = -k x extension
  | displacement from rest posn.
  +ve number called Spring Constant
• You squeeze spring it pushes outwards.
  You stretch spring it pulls inwards.
• Plot of force against length is a straight line so call this a Linear Force.
• Slope of line is spring constant k.

Sinusoidal Motion.

• Amplitude is max excursion.
• Period is time to repeat = 1/Frequency.
• Phase is when wave goes through zero.
• Energy is proportional to square of amplitude!

Energy.

• Types of Energy
• Kinetic Energy, Potential Energy, Heat
• Electrical & Chemical (related to PE), Sound (bit of both)

Energy.

• Types of Energy
  • Kinetic Energy, Potential Energy, Heat
  • Electrical & Chemical (related to PE), Sound (bit of both)
  • Heat is really a kind of localised kinetic energy but common enough to treat on its own.
• Kinetic Energy
  • Energy of movement
  • Name from a Greek word for motion
  • Energy a body has simply because of its motion.
  • Kinetic Energy = 1/2 m v²
  • The heavier it is the more energy it has.
  • The faster it goes the more energy it has.
  • Energy grows MUCH faster with speed than with mass!
• Potential Energy
  • Energy that an object has because of its position or state. There but not apparent.
    • E.g. Gravitational P.E. = m g h.
    • E.g. Spring P.E. = 1/2 k x2
  • k is the spring constant
  • x is the extension, the amount of stretch
  • the stronger the spring the more energy it has
  • the further you stretch it the more energy you store.

First Law of Thermodynamics

• The First Law states that the total amount of energy in a closed system is a constant.
• A closed system is one where we are careful to include all the same particles before and after the experiment.
• This is an absolute law. In centuries of searching no errors have ever been found.
• In most systems it means that the sum of the kinetic and potential energy is constant.

Spring/Mass Energy

• K.E. 1/2 m v² greatest as mass goes through equilibrium where it is going fastest.
• K.E. minimum at ends where mass is still.
• P.E. 1/2 k x² greatest at ends where spring is stretched most.
• P.E. minimum at center, where spring is un-stretched from equilib.
• So total K.E. + P.E. = Constant.
• Total energy is proportional to Amplitude².

Energy in a Sound Wave.

• Kinetic energy is in the movements of the air.
• Air is the mass and the velocity is the air moving from high to low pressure regions.
• Potential energy is stored in the springiness of the air.
• Air in the most compressed and most expanded regions has the most P.E.
• As the wave moves the energy is carried along at the speed of sound.

Making a Sound

• Need a source of energy. The sound is going to carry energy away so the first law says that we need to put some energy in to provide the energy for the sound.
• Need something to move the air around.
• Often have a resonator that alters the tone of the sound and its loudness. We'll come back to that in a minute.

Sources of Energy

• Transient source of energy leads to a transient sound.
  • Deposit a certain amount of energy and the sound starts to carry away the energy. As energy is used up the sound fades until it is all gone.
  • Hit something
    • E.g. piano, drum, xylophone, gong, cembalon
  • Pluck Something
    • E.g. guitar, harpsichord, pizzicato, mbira
• Prolonged source of energy leads to a prolonged sound.
  • Put energy in at rate sufficient to make up for energy carried off by sound so sound lasts.
  • Balance takes time to set up. At start is imbalance that you can hear.
  • Blowing--flute, trumpet, organ, accordion
  • Bowing---violin, psaltery, saw, tympani
  • Rubbing--gongs, tympani

The Driven Oscillator

• We have seen that a disturbed spring-mass system oscillates at a single well-defined frequency.
• If we excite the system at any other frequency then the system will respond at that driving frequency.
• The response will generally be small unless the driving frequency is very close to the natural "resonant" or "resonance" frequency.

Resonance

• The size of the response and its sharpness in frequency depend upon the friction in the system.
• We quantify the friction using the Q (Quality) factor.
• Q = Energy Stored in System
• Energy lost in 1 Period
• If there is very little friction in the system then the Q is high, the system makes a large response to the driving force, and the response is very sharp.
• If there is a lot of friction then the Q is low, the response small and broad--extends over wide range of f.

Resonance Curve

Comlex Oscillating Systems and Normal Modes

• Simple Harmonic Motion is exemplified by the spring-mass system. The position is a sinusoidal function of time with frequency
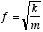
  where k is the spring constant and m the mass.
• A Normal Mode is a special motion of a system of particles in which all parts of the system execute Simple Harmonic Motion at the same frequency.
• A system with N masses coupled together will have N different normal modes.
• A continuous system, such as a bar, string, or skin, will have an infinite number of modes. The lowest modes will be the simplest motions and the higher modes will usually be too small and too high frequency to be of interest.
• Every motion of the system can be written as a sum of the normal modes.
• If we analyze the sound spectrum then we shall only find frequencies corresponding to the normal modes.
• The amount of each normal mode depends on the way that the motion was started.
• Modes whose shape is similar to the starting shape will be strongly excited, those with different shapes will be weakly excited.
• When the initial shape is produced by striking or plucking the system then those modes with anti-nodes closest to the striking point will be strongest and those with nodes closest to the striking point will be weakest.