

3) Prove that the medians of a triangle
intersect at a point one third of the way along each median.
Note. A median joins the mid-point of one side to the opposite corner of the
triangle.
Hint. Draw a good picture. Use two sides of the triangle as basis vectors.
4) If A = 2i + j + k, B = i - 2j + 2k, and C = 3i -4j + 2k, find the projection of A+C in the direction of B.
5) If A x B = A x C, does B = C necessarily?
6) A particle moves along the space curve r
= exp(-t) (i cos(t) + j sin(t) + k).
a) Sketch the curve of r.
b) Find the magnitude and direction of the velocity at any time t.
c) Find the magnitude and direction of the acceleration at any time t.
7) If A is a differentiable function of u and |A(u)|=1, prove that dA/du is perpendicular to A.
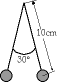
8). Using the diagram below find the magnitudes of the charges on the two spheres. The spheres are metal coated pith balls and are small enough that you can assume that the charge spreads evenly over their surfaces so that they act like point charges. Each pith ball weighs 5g and the strings weigh so little that you can ignore their weight.
2) The figure below shows three equally spaced charges (the small circles).
a) Find the Electric Field at the four points marked with an x. They are all on a square
grid of side l.
b) Sketch the Electric Field near the sharges (out to about 2l to 3l).
c) Sketch the Electric Field a long way from the charges, out to at least 20l away.
![]()
3) The figure below shows four charges placed on the corners of a square of side l.
a) Sketch the Electric Field near the charges (out to 2-3l).
b) Sketch the Electric Field far from the charges (to at least 20l away).
c) Discuss the relationship between the field in part b and field in part c of Q2.
![]()
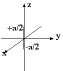
4) In class we found the field in the bisector plane near a short rod of charge. Use the same method to find the field outside the rod along the line of the charge. That is, find the field along the z axis in the figure below.
5) Consider the bisector plane of an electric dipole. For example, in the figure below, where the charges are +Q at +k and -Q at -k, this is the plane z = 0. First find the electric field on that plane. Then find the TOTAL flux that passes across that plane in the +ve z direction.
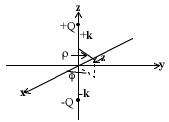
^) Find the electrostatic potential at all points in the bisector plane of the electric dipole in the figure above.
5) A charge Q sits at the centre of a cube of side a. Calculate the electric flux through one side of the cube by direct integration and also by Gauss's Law.
6) During Coulomb's lifetime there was considerable opposition to his theory that the electric force fell off as r-2. Such an authority as Alessandro Volta, the man who started the modern investigation of electricity, maintained that the field actually fell as r-1. Show that this would violate Gauss's Law. That is, show that if
![]()
then the integral of the flux over a sphere centred on the charge does depend on the radius of the sphere.
7) Consider a thin plastic rod bent into an arc of radius R and angle q'(see
below). This rod carries a charge
Q uniformly distributed along its length. Compute the electric field E at the
origin.
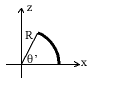
Do this in the usual steps:
a) Draw a diagram showing what variables you will use, how you will cut the rod into elementary pieces, and what the DE from an elementary piece looks like.
b) Express DE algebraically in terms of the variables and the unit vectors i, j, and k.
c) Write the total field as an integral with appropriate boundary conditions and evaluate that integral.
d) Show that your answer makes physical sense.
Note for 1.12. Draw a good diagram and assume that conditions in half a sphere are nearly the same as if the rest of the sphere were there. This will be true well away from the end of the hemisphere and can be made almost perfectly true by adding fine wire grids at the edges.
6) A solid plastic sphere of radius R1 has a charge -Q1 uniformly distributed over its surface. A concentric metal sphere with inner radius R2 and outer radius R3 surrounds the plastic sphere. There is a charge +Q2 on its inner surface and a charge +Q3 on its outer surface. The total charge on the metal, Q2 + Q3, is greater than Q1.
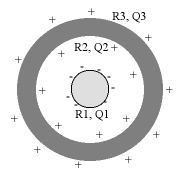
Use Gauss's Law to find the magnitude and direction of the electric field at various radii, r, from the centre of the solid sphere. Consider separately the cases
a) r < R1 (inside the plastic sphere), b) R1 < r < R2 (in the air gap), c) R2 < r < R3 (in the metal), and d) R3 < r (outside the metal).
If -Q1 = -5nC what can you say about Q2? Explain.
7) The potential far from an electric quadrupole is given by ![]() .
.
Find the Electric field that gives rise to this potential.(This is definitely easiest in spherical polars and you should use this as a chance to get practice with Appendix B.)
8) A thin, non-conducting, plastic rod is bent into the form of a nearly complete circle with a radius of 50 cm. There is a 2 cm gap between the ends. A positive chrage of 1 C is spread uniformly over the length of the rod. What is the magnitude and direction of the electric field at the centre of the circle? (Hint. Symmetry will help but you also need to remember that the principle of superposition works just as well for subtracting fields as for adding them. You should also note that you have found the answer to a related problem in the last homework that should be a great help in doing this.)
9) Two infinite plane sheets of charge, one of density s = 6 C/m2 and one of density s = -4 C/m2 are located 10 cm apart, parallel to one another. Describe the electric field everywhere in this system.
10) Some time ago we found the Electric Field from a finite length rod of charge in a couple of special directions by integrating the field from little lengths of the rod. Now write an integral giving the electric potential at any point in space. You should probably work in cylindrical polar coordinates and do not need to evaluate the integral.
6) Consider the electrostatic potential ![]() .
.
Please deduce and explain everything there is to know about V, E, and the charge distribution that produced them from an examination of V.
a) What do the equipotential surfaces look like? Sketch a cross-section of the equipotentials to show the spacing.
b) Use the relation E = -grad V to find the electric field and thus sketch the field lines.
c) Use the differential form of Gauss's Law to find the charge distribution
![]() .
.
d) This is a somewhat peculiar charge distribution. One expects that for very large r the system should look like a point charge but that would give a somewhat different potential. Can you say anything about why this is so?
NOTE this is a description of the electron density in a Hydrogen atom in its ground state. You may like to think about the effect of including the nucleus.
9) Here there are 6 pictures of electric fields. Which of them have div E equal to zero and which have non-zero div E? If some have non-zero div E indicate in what regions the non-zero divergence is found.
10) Explain what is meant by the terms "Linear" and "Isotropic" when referring to a dielectric material. What would be different about the behavior of a material which was NOT isotropic compared to a material that was?
7) An electron travelling with a velocity of 107i m/s enters the region between a pair of capacitor plates. The plates are squares, 10cm on a side, separated by 1cm in the z direction and have a potential of 1V between them (below). Describe the path of the electron as passes between the plates and find the angle at which it leaves the plates. You may assume that the field between the plates is uniform.
![]()
8) A wire carrying a current I lies along the z axis with the current flowing in the positive z direction. Verify the Ampere's Law holds for the rectangular path (-2, -1, 0) to (2, -1, 0) to (2, 1, 0) to (-2, 1, 0) and back to (-2, -1, 0). (Hint, with a little care you need do only 1 line integral.)
7) A very long straight wire of radius R carries a high-frequency alternating current. For reasons that we may come to understand, this means that the current is confined to a thin layer near the surface of the wire (skin effect). Assuming that the high-frequency has no other effect on the magnetic field, compute the magnetic field inside and outside the wire if the current density at radius r is given by J = J0 exp((r-R)/d) where d, the skin depth, is smaller than R.
5) 6.5) You need not do part (i) since we have not formally studied magnetic materials (though I encourage you to read Chapter 5).
7) A circular metal disk of radius R rotates with angular velocity w about an axis through its centre perpendicular to its face. The disk rotates in a uniform magnetic field B whose direction is parallel to the axis of rotation. Find the EMF induced between the center and the edge.
8) Find the magnitude and direction of the electric field at all points in the disk in question 1.
9) A conducting rod of mass m and resistance R rests on two parallel frictionless rails a distance l apart (see figure). There is a uniform magnetic field B perpendicular to rails and rod. At time t=0 the rod is given an initial velocity v0 parallel to the rails. Find the subsequent speed of the rod a) if the rails are insulated from each other and b) if the rails are connected at one end by a wire with no resistance (so that the rod's resistance is the only resistance inthe circuit).
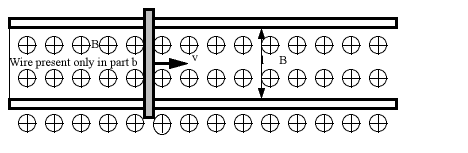
10) Consider the rod in part b of the previous question where the rails are connected together. Show that the power needed to move the rod along at constant speed is P = Fv = B2l2v2/R and compare this to the power (P = I2R) dissipated in the resistor.
5) If magnetic monopoles existed, which of Maxwell's equations would be altered and what would be their new form? You should use Qm for the magnetic charge corrseponding to Q for an electric charge and similar names for other quantities (e.g. magnetic current would be Im).
6) Consider a parallel plate capacitor with circular plates of radius R placed a distance d apart. They are connected at their centres to straight wires that extend perpendicularly from the plates.
a) Show that the magnetic field at a radius r out side the capacitor plates (that is r > R) is given by
where ID is the displacement current.
b) This is the same formula as for the field outside the wire leading to the capacitor, why?
c) Compare the magnetic field between the plates with the field outside the wire. Calculate both fields at the same radius r > R. Discuss whether this makes sense.
d) What can you say about the relative strengths of the fields inside the capacitor and outside the wire for radii r < R?
7) A superconducting DC power transmission line has been proposed that would caryy 100 gigawatts of power at 200,000V over 1000km. The conductors would have a diameter of 25mm and be separated by a center to center distance of 75mm..
a) Calculated the force per meter between the conductors. (It would clearly preferable to use a co-axial line!)b) Calculate the amount of energy stored in the magnetic field. Give your answer in kilowatt-hours. Remember that energy stored = (L I^2)/2 and note that the self-inductance of a pair of parallel conductors of radius R separated by a distance D is .
8) A long solenoid, length L, has a single layer of turns, N per meter. By considering the energy stored in the coil, calculate the force between one turn and the next. Does this force tend to compress or expand the coil?
Last modified 8/10/2000.
For questions or comments contact
Brian Collett
Physics Department
bcollett@hamilton.edu